Canada Olympic Trials: AKA Roar of the Rings

It was an enjoyable week for fans in Edmonton, but not necessarily for 14 of the teams participating. Four years of hard work, practice, travel, and time away from family and jobs, all culminated into one intense week of curling. Ultimately only 8 remaining players (ok, 10 if you include the 5th man/woman) experienced the thrill of victory. The remaining squads are left to wonder what could have been.
Speaking of the 5th position, will the CCA approve of the current extra teammates? Will the teams keep them or toss them aside? Does it really matter? Not for me to ponder I’d prefer to look at specific games and some of the decisions made throughout the week.

1. Randy Ferbey vs. Glenn Howard
Ferbey was 9-7 against Howard going into this game and needed a win to ensure their game against Koe Thursday night would have play-off implications.


5th End: Russ Howard (commentating for TSN) questions Ferbey’s decision to come into the rings on David’s last shot. A valid point and Randy’s squad is fortunate to get away with only giving up a single.

Ferbey is Red

At this stage, Ferbey is up 4-2, Howard has last rock. If the freeze attempt by Nedohin is perfect, Howard is likely forced to one. He could attempt a difficult double raise but more likely may try a delicate draw to the edge of the button avoiding the corner guard on the in-turn. Most likely Howard gets one and Ferbey is up 4-3 with hammer and 5 ends to play. In this situation his Winning Percentage (WP) is 80%.


If Ferbey instead throws a guard, he could cut-off Howard’s in-turn draw and make it difficult for him to get two. Glenn would have to play an out turn and try to catch half of the four foot. If we assume Glen makes his deuce 100% of the time, game is tied and Ferbey’s WP = 61%. If Glen gets three or four, which was possible given where David’s rock ended up, Howard’s WP is either 60% or 75%. Ultimately Ferbey is trying to gain Dominant position (80% or greater) rather than stay in a close game (<66%) at the risk of putting Howard in Control (>66%<80%).

I’ll spare everyone the formula (let me know if you’re interested), but Dave needs to make this corner freeze roughly ½ the time for the call to be correct.


9th End: Alan Cameron may have misquoted me slightly in his article: (http://communities.canada.com/calgaryherald/blogs/curling/archive/2009/12/12/numbers-favour-martin-in-final.aspx). What perhaps I meant to say was “if you agree with Randy’s assessment of David’s chance to make that shot (4 or 5 out of 10) then it is the correct call”. Alternately, if you agree with Russ Howard’s assessment of Dave’s chances as 10%, then it is not. How often does he need to make the shot to make it the correct call?

If Ferbey takes one, WP = 25%. Taking stats exclusively from Grand Slam events show this number is closer to 20%. This is the only significant difference in numbers we see from Grand Slams versus all events. We’ll use 25% for now.

.25 = .6x +.12y +.01z +.25s

Where
x = estimate the double is made for two
y = estimate Howard steals 1
z = estimate Howard steals 2
s = Ferbey takes 1


And x + y + z + s = 1


Let’s chose z as 10% and s as 5%.

.25 = .6x + .12(1-x-.001-.0125) + .01(.1) +.25(.05)

Solving for x = .246 or approx 25%.


If we assume s is 0 and z is 20% it only increases to 27%. Giving up a single or a steal of two to Howard has minimal difference in the probable outcome.


If we also think our chances of stealing in the 10th end is less than 25%, we are even more inclined to try the double. If we think we will only steal 20% (similar to Grand Slam numbers) then x = 14% or 16%. This is still above Russ Howard’s estimate, but well within range of Randy’s.


2. Kevin Koe vs. Glenn Howard
In the 9th End, Koe, trailing 5-4, is faced with a similar decision as Ferbey was in the previous example. Rather than draw for his single, Koe elects to play a soft out-turn take-out around the guard in front of the rings. It’s an attempt to score two but a miss results in a steal. No steal of two here, and perhaps some small chance his draw for one would be missed (needed full four foot). The hit he played could also possibly result in a single, but very difficult given that they were pushing shot stone towards the button. I’ll leave the calculations up to the reader, but appears their chances for two needed to be close to Nedohin’s in order for it to be the correct call.

Koe is Red
3. Koe vs. Gunnlaugson

Easily the most entertaining 7-2 game I’ve seen in a long time.

3rd End: Koe is up 1 without hammer. There is a single tight corner guard way out on the wing. Koe attempts a draw around on his first rock and comes light, leaving two stones staggered. Jason decides “because it’s the 3rd end” to draw to the open. The end is blanked. This is simply a case of over thinking a philosophy which I’ve heard before about “scoring in the even ends”. I even discussed some of this in my article from February 2009. In it, I discuss the 5th and 8th ends. Notice the 5th end is an odd numbered end; however in that article I argued preference to have the hammer.

Gunnlaugson is Red

A score here by Jason and a Koe score in the 4th gives Gunner hammer back in the 5th. An example: If Jason scores 2 here and then forces Koe to one in the 4th he is tied with hammer entering the middle game (5th end) and has 61% WP (Close Game). If Jason scores two in the 5th, his WP = 75%. If he waits to the 4th and holds Koe in the 5th, his WP = 62%. If he then scores two in the 6th, his WP increases to 79%. Interestingly enough, this is a .04 difference and shows Gunnlaugson does gain if scoring a deuce in the 4th instead of the 3rd. However, both are still in what I define as Control and not a Dominant position. And the overriding factor is, there are too many “IFs”.

All we specifically know at this stage is the chances at the end of the 3rd end: Blank WP = 43%

Jason scores two WP = 61%

Gunnlaugson takes one WP = 39%

Koe steals, Jason’s WP = 26%

In order for the call for two to be correct:

WP = .61x + .39y + .26z

Where

x is a deuce for Jason

y is a single for Jason

z is a steal for Koe

We can likely assume the chance Koe steals is very small. Jason would only need to bite the eight foot to take one. Let’s assume z=0

WP = .43 = .61x +.39(1-x)

Solving for x = 18%.

Bringing a possible steal into play, we could estimate Jason needs to make his deuce more than 20% of the time to make the attempt at a deuce correct.

These WPs are also based on average numbers and I’ve stated before that the more ends remaining, the greater disparity from the average for teams of unequal strength we can expect. We can assume that Koe is a stronger team; however we can still compare the values and determine which decision leads to a better outcome.

The only possible argument to be made is that with fewer ends remaining, the result will be closer – but it is only one end less so it is not significant enough to sway our decision. For example, if you are a weaker team and win the toss, my theory would indicate your best chance may be to blank 9 ends and then be tied with hammer in the final end. This eliminates the chance your opponent will can use their superior skill during the many ends available to score multiple points. With free-guard zone however, this is simply not possible. At any stage your opponent can force you into a non-blanked end.

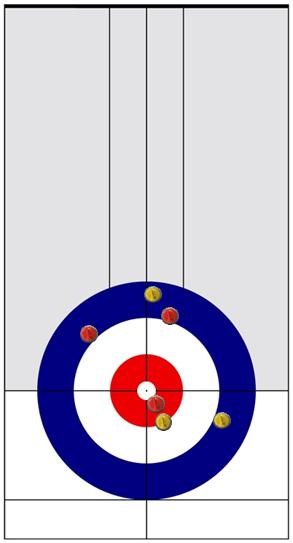
5th End: I’d nominate the 5th end in this game with the 9th end in Howard vs. Middaugh for “Best Ends” of the week. See image which shows the rock placement before Jason’s first stone.

Gunnlaugson is Red

There were multiple calls which could be argued several ways and all opinions could likely be supported. One thought I’d like to bring up was Jason’s comments heard on CurlTV of a “big end” vs a deuce. Should they position for a “big end” or try for the deuce?

At this stage, Gunnlaugson is two down with hammer. Here are various WPs at end of the 5th, based on possible outcomes from this end:

Koe steals, Jason’s WP = 11%

Single WP=20%

Deuce WP = 39%

Three WP = 61%

Four WP = 75%

I won’t even begin to analyze the possibilities based on rock position, etc. Have fun if you like. In general, I like Gunnlaugson playing for a big end based on the fact that he expects his opponent is stronger and the positioning of the rocks are such you may be able to take some risk and put the game back to Close or with a 4, take Control. If I’m the stronger team I would be more inclined to take my deuce and use my skill to create opportunities in the last half of the game. Unfortunately, Jason wasn’t able to make the big shot or place the rocks correctly to get the big end. Hats off to Kevin Koe who made a brilliant shot on his last to take away most of Gunnlaugson’s options.

4. Kevin Koe vs Kevin Martin

Martin is up 6-5 with hammer in the 9th End. On John Morris last rock Kevin Martin elects to keep the centre guard and play into the rings (see image). Why doesn’t Martin peel the guard here? If Kevin takes one or blanks, he leaves Koe with an 11-12% chance to win. If Koe steals it goes up to 20-25%. If Koe steals 2, as unlikely as it would appear, Koe now wins 60%.

Koe is Red

Kevin’s thinking could be:

“If I peel twice, Koe will hit on his last rock. I’ll face three and have to play a double and likely give up a   steal. If I play into the rings now, I at least give myself some chance to score and it is doubtful Koe could steal 2, which is my primary risk”.

During the CurlTV broadcast I questioned the call, preferring to peel. In retrospect, you can make a good argument for both decisions.

5. Glenn Howard vs. Wayne Middaugh

Wayne had a tough week. His first three games were Ferbey, Howard then Martin. He needed to come out of those three with at least a win but never got any momentum. The Howard game was a close one which could have gone the other way.

9th End: The 9th end was (along with Gunnlaugson vs. Koe 5th end) my vote for most exciting end of the event. It lasts nearly 25 minutes!

Check it out at http://www.tsn.ca/curling  and link to Video.

The view of the house before Wayne throws his last rock...

Howard is Red

Howard is up 5-4 with hammer and elects to leave the long guard. This gets them into some trouble and they nearly give up a steal of two. See analysis above in Koe vs. Martin and think if a similar decision comes into play for Glenn at some point in the end.

6. Glenn Howard vs. Kevin Martin, Round Robin

Clearly the best game of the week. Unfortunate the final didn’t live up to the re-match we’d have wanted.

8th End: Martin is tied 5-5 without hammer and elects to play his first rock in the rings rather than play a centre guard. I wrote about this in several previous articles, including January 2009. Kevin is still the only top skip I’ve seen make this play.

Howard is Red

Martin’s final shot in this end was the shot of the week. Facing a 2 or possible three by Howard, Kevin makes a fantastic hit and roll, corner freezing to his own stone. Howard still has a raise for a multiple score but it is much more difficult and he is held to one instead of the game being possibly over. Because it’s tied in the 8th end, Kevin knows that whether Howard scores a two or a three it has little bearing on the outcome, they will likely lose the game.

What is interesting in this scenario is both the ability to visualize the shot and the dynamic between John and Kevin. At first Kevin didn’t like the out-turn. John was able to maneuver the conversation and ease Kevin into the decision, without challenging him. It is generally accepted that you don’t want your skip playing a shot he or she is not comfortable playing. This discussion captured parts of the game that are critical to success and can’t be simply analyzed by numbers.

Further to this, I’d suggest Curling is made up of 4 key areas:

1. Physical Skills

  a. Throwing the rock

  b. Sweeping

2. Mental Skills

  a. Reading ice and rocks

  b. Communication

     i. Calling line

     ii. Judging weight

3. Strategy

  a. Calling the game

4. Psychology

  a. Emotional control

  b. Team chemistry

My blog focuses almost exclusively on Item 3. This is an example of item 4. In these cases, teammates become like a caddy who is discussing which club to play on an important shot. It’s not always about which club is correct but about how the caddy interacts and builds confidence in the golfer. These areas are ranked by what I would consider level of importance, although top teams are generally strong in all areas.

If you’d like to review video from any of these games or others, check out http://www.curltv.com/ or http://www.tsn.ca/curling and click on Video.

Have a Safe and Happy Holidays!

Canada Olympic Trials Preview – and Coming Soon to CurlTV…

Yes readers, yours truly, the Curl with Math guy (perhaps a better moniker would help my marketing efforts), will be joining Luke Coley in the broadcast booth for several draws during the Roar of the Rings! Actually, I prefer the name “Olympic Trials”, as it more clearly states what is actually going on. ROTR seems to be a screenwriter’s pitch to Warner Brothers for a new movie…. “Lion King meets Lord of the Rings….and we’ll film it in Edmonton; parts of it look just like Mordor and the locals look like Hobbits”.

Let’s begin our Preview show…

Men’s Teams
The “Big Four” are Martin, Howard, Ferbey and Stoughton. No slight to Middaugh, who is a two time Brier champion or Koe who is an original 4 qualifier, but those four teams have the most wins, best records and greatest success against the field going back many years. It would not be a surprise if any of these teams won, and the numbers will show us why.

The Favorites

• Kevin Martin is 76-35 (68%) since start of the 06/07 season against this field and is 41-19 (also 68%) against the rest of the Big Four.
• Howard is 13-13 against Martin and 7-8 since 06/07. However, they are also .500 against the others in the Big Four, 31-31 overall and 17-17 since 06/07.
• Martin has outscored all Trials teams by nearly a point per game. Howard and Ferbey are around a half point.
• Martin is 22-18 against Stoughton historically but 11-2 since the 2007 Brier.
• Provincial Rivals – both Favorites have been dominant:
• Martin is 20-7 against Ferbey since 06/07 and 27-10 overall.
• Howard is 12-5 since 06/07 (70%) and 25-14 historical numbers against his ex-teammate, Wayne Middaugh.

Contenders

• Ferbey is only 16-29 (36%) since 06/07 against other Big Four teams but minus Martin, they are 9-9 against Stoughton and Howard since then and 21-17 overall against those two teams.
• Stoughton is 80-74 against the entire Field but has beaten Gunnlaugson (including Carruthers) 10 times. Jeff is 37-46 overall against the other Big Four teams including a mere 13-22 (37.1%) since 06/07.

Challengers

•  As a top 4 qualifier Koe has a (somewhat) easier start, not facing Howard, Martin or Ferbey until their final three games. Their opening game is against Simmons, against whom they are 11-0. They are 7-6 vs Stoughton but against Howard, Martin and Ferbey they are 18-41 overall and 18-37 since 06/07.
• Middaugh plays Martin well (11-12 and 4-4 in last 3 years) but Howard (see above) and Ferbey (4-11) both seem to have his number. Middaugh is 7-0 vs Carruthers/Gunnlaugson.

Underdogs

• Simmons, is he an underdog? Numbers indicate yes. They have only won 32% against this field and haven’t shown to be any stronger since 2006. They are 5-1 against Middaugh in the last few years and…if they can finally win against Koe… 
• Gunnlaugson has no chance, mathematically. But then again, Gushue probably didn’t have much chance last time either, even Stoughton said so…. With their small sample size, we don’t have much to analyze. Including Carruthers, Daley Peters and Gunnlaugson as skipping the squad is 12-37 against this field. However, Gunner is 3-5 as a skip and has beaten Howard, Koe and Stoughton. If only he’d picked up a veteran to play front end….

Play-off Bound?
Let’s examine chances of outcomes. These are based on handicapping analysis I have done. I will spare you the details of the numbers, other than to say if you’d like to bet on any games, please let me know.

• Martin has 7% chance and Howard a 4% chance to go undefeated.
• At least 5 Wins – Howard is around 54%, Martin near 65%. Next closest is Ferbey at 32%.
• At least 4 Wins – Howard is 80% likely, Martin 86%, Ferbey 62%, Stoughton 58%
• Koe is 49% likely to get to 4 wins, Middaugh is 45% and Simmons 16%
• Gunnlaugson is calculated at approximately 7% chance at 4 Wins. As I stated earlier, this is based on small sample size and with other skips, so if someone offers you better than even money that Gunner will win 2, then it is a good bet. Of course, he still might go Winless (12% chance).

Women’s Teams
The Women’s Trials teams have the Big Two but also 3 others who are very close. Jones and Lawton then Scott , Bernard and Kleibrink. Let’s call them the Top 5.

It would not be a surprise if any one of these five finished as the winner. It should be noted, the sample size (or numbers of games played) amongst these teams is far smaller than those for the Men’s. This leads to more variability in probable outcomes. But let’s still take a look…

The Favorites

• Jones is 39-23 (63%) and 29-21 against the other top 5 teams. She is 8-1 against Bernard, 4-0 against McCarville but 6-9 against Scott.
• Lawton is 38-25 against this field including 27-19 (59%) against the other top 5. They are 9-3 against Scott and 0-3 against McCarville
• Heads up Jones edges Lawton 6-5.

Contenders

•  Scott is 33-30 against the other Top 5 and 12-5 against Bernard. Interestingly, she’s only 2-5 against Holland.
• Kleibrink is only 41% against the other Top 5 and, though 10-9 against Scott they are 7-3 in the last 10 meetings.
• Bernard is 40% against the other Top 5. Strong against her Calgary opponents: 8-4 against Kleibrink and 6-0 against Webster.

Challengers

McCarville’s numbers are close to Kleibrink, Scott and Bernard. They are 46% against this field while the others are 48-50%. However, her sample size is much smaller and we can expect her success at this level of competition is not on par, so we will put her in this category (so that we have someone!).

Underdogs

•  Webster played well at the Pre-Trials, qualifying in A, but historically they are 10-24 against this field. It’s not likely, but if given the right odds, some would say it’s good to bet a streak.
• Holland is 16-27 against these teams but is 5-2 versus Scott. Being the last qualifier they have a tough start but who knows….

Play-off Bound?

• Jones has a 6% chance and Lawton a 4% to go undefeated.
• At least 5 Wins – Jones is 59%, Lawton is 50%. Next closest is Scott at 25%.
• At least 4 Wins – Jones is 84%, Lawton is 78%, Scott and Bernard 53%, and Kleibrink (50%).
• McCarville has a 47% expectation for 4 wins and Holland is 25% likely.
• Webster is 11% likely to get 4 wins and 9% likely to be Winless.

Predictions
So now that we’ve looked at the records, who do I like? The correct answer is always whoever gives me the best odds, but if we aren’t taking Gunner at +380 to beat Stoughton, then I suppose I’ll go with my gut (and not my wallet)…

Howard, Martin, Ferbey all get in the play-offs. 2006 was an anomaly and these guys are all more prepared and playing better against the field coming in than they did in 2006. I think one or two others may also be in tie breakers, likely Stoughton and possibly Middaugh – but he needs a good start. Koe has a chance to get on a roll with some early wins but will need to hold on. Simmons had a good Pre-Trials but they may get called for too many men on the ice. I think if Gunner goes 0-7 its possible to have a 6-way tie at 4-3. Wouldn’t that be something?

Women’s? I don’t watch/study this game as much and think anything is possible. Many of these teams have the big game experience and should be able to play to their potential despite the magnitude of the event. The qualifying format through a Pre-Trials likely helped teams like Webster and McCarville in this regard and make them possibly more dangerous than some would suspect.

Play-off predictions?
I’ll wait until Thursday.

Note: the accuracy of these records is the responsibility of CurlingZone. We may be out by a game or so, but we have to start somewhere. If anyone has numbers which contradict these, please e-mail Dallas or Gerry @ CurlingZone.com.

Another note: These numbers don’t rank the value of a win based on the importance of the game. For example, a win or loss could come in the Brier or in the opening round of a WCT cashspiel. We could try to add this to our analysis, but I do have a day job and I don’t know how much more value it gives us.

And yet another note….

PLEASE, PLEASE, PLEASE…will PinnacleSports or some other betting web site offer the Canada Olympic Trials? Four years ago some great gambling opportunities and the Brier last year was a potential gold mine. And finally, this year, I do all the prep, analyze the records, am prepared to lay down my money….and no where to put it. Guess we’ll have to wait for Vancouver….

Two other Math notes this month…

1. There should be no surprise that I agreed with Bill Belichek’s call on 4th and 2 versus the Colts a few weeks ago. For anyone wanting math analysis in Football, check out http://www.advancednflstats.com/ and their coverage of that controversial decision at http://www.advancednflstats.com/2009/11/belichicks-4th-down-decision-vs-colts.html. Of interesting note is how talking heads (of which I will be one next week) try to attempt to support their belief regardless of the actual numbers. Tony Dungy said that Bill “should have gone with the percentages” and punted. Actually Tony, percentages say the opposite. The following weekend on ESPN Sports Reporters, Mitch Albom of the fine quaff and author of such books as Tuesday’s with Morrie, Five People You Meet in heaven, and other books which can be made into an ABC Hallmark movie of the week, said “No, it’s one of those things that if it works it’s the right call. It didn’t work and every single number out there that you can crunch says it was the bad call.” What?
2. Troy Aikman this past weekend mentioned, while commentating on my Vikings, that coach Brad Childress should be concerned that Favre has only thrown 3 interceptions this year and he is likely due for a bad game where he will throw 4 or 5. We hear nonsense like this all the time in baseball when the announcer says “he’s 0 for his last 5 at bats, he’s due for a hit here”. These examples are similar to stating that if a coin comes up heads 9 times then it is more likely to come up tails on the 10th attempt. I hope my readers have figured out that is not the case.

If you happen to be at the Trials in Edmonton and read my articles, whether you agree, disagree or really don’t care, please come say hello. I’ll be the person in the CurlTV booth most likely to be fired.

Notes from the Pre-Trials (AKA “Road to the Roar”)

I’m struggling with this event called the Road to the Roar or more aptly named Pre-Trials. It reminds me of the NFL deciding to increase playoff teams from 10 to 12 in order to generate more games (and more revenue) on opening “Wild-card” weekend. It’s not that the entertainment isn’t there, but why not just have 16 teams at the Trials in December? Money must have something to do with it. Or perhaps the 400 or so people in the stands in Prince George demanded their opportunity to shine in the spotlight.

Some random thoughts and analysis….

1. TSN please show me the first stones of the end! Not doing so makes it hard to understand what strategy is being played. I couldn’t tell if Gunnlaugson had some strange calls or they just missed shots. In 7th end Gunnlaugson is up one without hammer (5-4) and plays a centre guard, rather than in rings. Perhaps he read my article from February 2009 where I stated “If we are one up in the 4th or 7th, we should force our opponent into scoring, even at the risk of a deuce, in order to have hammer in following end.”

2. During the 9th end of the C Final between Gunnlaugson and McEwen, Linda said "hammer is still the advantage in that last end”. This isn't quite correct as a team would prefer to be one up without hammer vs one down with. The correct strategy is to play for a steal at the risk of a deuce in the 9th end, and if you force your opponent to one you increase your chances to win from 60% to over 75%. I didn’t see if Jason intended to play their first rock in the rings because, per note 1 above , TSN didn’t show it! I don’t like the 9th playing out the way it did for Jason. Much better for him to be aggressive in this situation.

3. Simmons vs Stoughton, A Final. Interesting choice by Simmons to hit and roll in the 8th end. It appeared he could have played a draw and sit shot stone frozen to the Stoughton rock behind the button. Possible he was concerned by lack of curl or afraid of leaving the angle raise or other shot for a big end.

 Stoughton is Red

This is an important point in the game. Simmons is two up and holding Stoughton to one is a huge advantage. Simmons chances of winning goes from 67% (tied with hammer and just barely Control) to 86% (and Dominant Control) if he holds Stoughton to a single instead of the two he surrendered. Even if Stoughton makes a circus shot and takes three, Simmons still has 37% chance to win. I prefer the draw for these reasons and if he comes short he still leaves a very difficult shot for two.

4. Yes Mike McEwen, you should have played the double in the 8th end against Jason Gunnlaugson in the C Final. Your margin for error was substantially smaller with the hit and stick you attempted. Also, you left your opponent a chance, the other option did not. Kevin Martin would have removed both those stones before you got in the hack. I suspect in years to come you will also.

McEwen is Red

 5. The B Final, 8th end. Simmons is up 5 to 4, McEwen has hammer. Simmons plays the run-back again on his last shot.

 McEwen is Red

He could have chosen to draw instead. A successful run back likely forces Mike to one anyway. It appeared an out-turn draw to the face of the stone could provide the same outcome with more margin for error. However, the amount of curl may have weighed in on the decision. Let’s take a look at Pat’s thinking:

Draw: Let’s expect Pat makes a reasonable attempt to draw to the face of Mike’s stone but Mike makes his draw 50% of the time.

W = .5(.67) + .5(.37) = 52%

Run-back: How often does Pat need to make the shot for it to be the correct call?

W = .52 = x(.67) + (1-x)(.37)

Note we assume Mike always scores two – in the actual game his rock caught debris and he did not, but that is assumed to be minimal for our analysis and then can be factored into our decision later.

We can see that if x (Pat’s chance of the run-back) is greater than 50% then it is the correct call. If we assume Mike makes the draw 60%, then x = .4 and Pat only needs to make the runback 40% for it to be the correct call. Further examples show it as a linear equation in that Pat needs to make his shot more often than Mike misses a draw for it to be the correct call. The readers can decide if Pat made the “correct” choice.

6. Same game, 9th end, Simmons plays a corner guard? Interesting call (unless of course he was light). Stating that he prefers to score multiple points at risk of a steal, rather than leave a possible blank open.

7. Same game, same end. McEwen’s first stone, he plays a run-back of the centre guard to Simmons rock in the top four. Giving up a deuce here is not good (less than 12% to win). Mike must hold Simmons to one or possibly steal.

McEwen is Red

I like keeping the centre guard in this situation, if only to keep the middle protected. At this late stage, he may have felt there was no good placement in the rings and he may be correct, but see how this decision drives the next decision? Even if he makes the shot (which he did, but was unfortunate the jam) Pat still can make another strong come around (which he did) and put himself in good position for two.

On Mike’s last I’d almost prefer a draw to either freeze or the back four foot.

McEwen is Red

As difficult as the shot is, the run-back needs to be a double. The issue here is, a deuce or a three have nearly the same outcome: you are very unlikely to win the game. The interesting analysis here is, Mike deciding to run-back on his first was already setting himself up for another run-back on his second. In essence, by calling it once, Mike is saying “I will make this shot twice” In making that decision, might be wise to determine your odds for making a run-back (ahem) back-to-back. If your chances are 90% of making one, then two in a row is (.9)x(.9) = .81 or 81%. If you only figure 80%, then you drop to 64% to make two in a row.

8. I grew up a rink rat at the Assiniboine Memorial in the mid 80s, watching Kerry Burtnyk. One of the classiest champions curling has ever seen. Kerry’s loss to Gunnlaugson was heart wrenching. His last rock in 10 needed only to roll an inch, it did not. Then a draw to the full eight turned into a burned rock, ending Kerry’s chances at an Olympic medal. I was hoping to see Burtnyk in Edmonton, but it is not to be. We can only hope he makes another run or two at a Brier bid (a la Werenich in 1995 and 1997).

9. Back to McEwen vs Gunnlagson, C Final. In the 8th end, up 6-5, Mike appeared to be in good position, sitting first and second on BJs first rock. They called time out, thought for a while, then peeled a corner guard.

McEwen is Red

I was unclear to their thinking here, other than it seemed like the best idea at the time. It didn’t appear to have much impact on the end. Alternatively, they could have chose a more aggressive play, either draw to open side or play some type of tight guard or draw. The rock they were concerned about (top yellow) did come back to haunt them later in the end. Mike commented they would have to make “a lot of good shots to get two” and, as often happens at this level, they did. The best part of their decision was avoiding 3, so we can’t fault them for that. And as I said above, if Mike had just played the double on his last….

10. Interesting choice by Jason to play a centre guard when one up in the last end without hammer. Mike doesn’t bite (perhaps Jason wanted him to?) and choses to play a corner guard rather than draw to centre.

Good luck to all in the “Actual” Trials, which I suppose we could now call the “Pre-Olympics”. Final thought…..is it too late for some young team to pick up Russ Howard?

New Season Begins and World Cup Final: Koe vs. Howard

Well, the new Curling Season is here and though I’m disappointed in the end to golf season I am anxious for the Olympic Trials. The Olympics themselves, sadly, I’ve never had much interest in. Why is it every four years I’m suppose to get excited about sports which I’ve never cared to watch during the past 1460 days since the last Olympiad? I never tuned in to CBC for skiing during the World Championships in 2008, so why now? If not for Curling, Hockey, and perhaps women’s’ short track speed skating (it’s like a cat fight on skates!), I’d likely pass on the entire thing completely. And don’t even get me started on the Summer Games – days on end of coverage from multiple networks, journalists, etc – and the only thing worth watching is 9.7 seconds of men running and a couple of laps in a pool (which took slightly longer). Better to watch the highlights on the internet after it’s all over.

In any event, we’re back into the “sweep” of things and need to begin.

1. Shorty Jenkins: Martin vs. Matchett
Gerry Geurts of CurlingZone relayed this shot call to me and he may have not remembered exactly right, but the analysis should still be interesting. In the semi-finals at the recent Shorty Jenkins event, Kevin Martin was one down playing the 7th, with hammer, against Dale Matchett. Matchett had a rock in the outside rings, perhaps biting eight foot, and there was a slightly off-centre guard. Martin, on his first stone, chose to play for his deuce by drawing around the guard. Remember, this is an 8 end game and only the final end remains. Kevin is forgoing an attempt at a blank, attempting to take two, with an increased risk of being held to one or even giving up a steal.

The chance of winning up one without hammer coming home is roughly 60%. If held to one, Martin’s chances drop to 25%. The difference in outcome between a successful two or held to one is greater here than at any point during a game. Let’s look at each option:

Draw: Assuming the draw takes away any chance of a blank, let’s determine how often Kevin must get a deuce to make this a correct call.

W = d(.6) + s(.25)

Where d = chance of a deuce and s = chance we are held to one. Assuming these are the only likely outcomes (blank and steal of two not likely), we solve for s= 1-d

W = .6d + .25(1-d).

To complete this calculation, we need to compare against the scenario if Kevin hits the stone.

If Kevin hits the open stone, Matchett either hits the Martin stone (trying to roll behind the guard I expect) or simply draws around the guard attempting to force Martin to a single point.

What likely entered Kevin’s thought process “if I hit and stick, Dale will draw around the guard and now I may be forced to one. My chances are better at two if I force the play now.”

When guessing what an opponent may do, we can estimate what the chance is they will make a certain play and evaluate further. For example, let’s start to analyze what happens if Kevin hits open stone.

Assumptions:

• Martin will always hit and stick successfully.
• If hit and roll succeeds, Martin always draws for one successfully (assuming the roll puts the rock in the back rings).
• If hit and roll doesn’t succeed, a blank always occurs.

Let’s first examine what happens if Matchett draws or hits:

Where:
x = Odds of winning if tied without hammer = 25%

y = Odds of winning one down with hammer = 40%

z = Odds of winning if two down with hammer = 12%

Hit: Estimate a roll successful 25% of the time.

W (Martin) = x(.25) + y(.75) = .363

Draw: Estimate with a draw Matchett steals 20%, Martin takes one 60% and he gets a deuce 20%…

W (Martin) = x(.6) + (1-y)(.2) + z(.2) = .294

Matchett should draw (based on our estimates are correct) – but perhaps he will only draw half the time. Then we weigh the chance of winning as:

W (Martin) = .5(.363) + .5(.194) = .33%

Therefore, using this in our original equation:

.33= .6d + .25(1-d) solving for d = .23

Therefore, Martin only has to get his deuce 23% of the time in order for the decision to be correct. Note that if Matchett always plays the draw, then Martin needs to make a deuce even less often (12.5%):

.294 = .6d + .25(1-d) solving for d=.125

2. Masters Final: Koe vs. Howard
It was an entertaining game last Sunday with Howard winning yet another Grand Slam. This was clearly one that could have gone the other way. An early steal of two had Glenn and his squad battling back. There were some timely misses by the Koe rink, but also some interesting decisions which may have provided them better opportunity to clinch a victory rather than being a bridesmaid for yet another Grand Slam final.

Some observations….

Second End:
Matt Hames in his Curling News blog suggests Koe could have played the in-turn draw instead of leaving Howard an opening for one…
http://curlnews.blogspot.com/2009/10/world-cup-sweeping-rant.html

I would tend to agree. At this stage he’s 2 up and if he does make a poor shot, at worse Howards gets a deuce and Koe’s odds are at 61% tied with 6 ends remaining. A steal would have put the Koe rink at odds of 89% chance to win. That is a chance you want to take during the Early Game, IMHO.

Third End:
Blake throws two draws. One appears 20 feet heavier than the next (according to the assessment by announcer Mike Harris). The sweepers are surprised and there is some discussion that his stones aren’t matched. How can teams at this level not have properly matched stones in a final of this type of event? Situation seemed very strange.

Fourth End:
Koe appears to be sitting third stone in the top eight foot, Howard is first, second and fourth. Kevin calls a hit on his own stone (driving it onto 4th rock), rolling across the house to then double the Howard stone. If successful, Howard would have a shot to hit and stick and sit two. Koe then would have had a double to force Howard to one. I thought the correct call on his first was the one he played on his final stone. Double the 1st and 2nd rocks and roll behind his other rock. If successful, Howard would be left with a choice to either draw around Koe’s top stone or attempt a difficult hit which appeared to be unlikely to allow him to sit two.

Sixth End:

Howard places a centre guard. Please see my articles from January 2009 and March 2009 for the analysis of why this not the “correct” call. I wonder if it was an intentional decision on the part of Howard to choose an alternate strategy, or if he is unaware of the analysis.

Interesting call on Howard’s first. Rather than hit the open stone, he plays into the centre and leaves a (albeit) long run back double for Koe to lie two. This is not a good position to give up a deuce, Howard’s odds of winning would drop to

15% if Koe pulls out the miracle. The flip side is, a steal of one for Howard puts the odds at him winning to 63%. Howard’s call into the rings on his last was clearly an intent to tempt Koe into a big weight shot rather than a draw. He could have instead placed a guard, leaving him a draw – but Koe may have hit no matter what the result. Also, a poor guard could have left a soft double with the inturn and a possible deuce for Koe.

Seventh End:
Blake’s second shot, after much debate, Koe’s team agrees to play a run back. In their position the centre guard is a critical stone to help plug up the four foot in an attempt to force Howard to one. The risk of a deuce is worth the attempt to steal or force a single. Playing the run back was an attempt to take a three out of play – which ultimately succeeded. However, if Blake plays a freeze, Howard may again play a draw, but more likely remove the guard and give Kevin a chance to clear the house on his first shot – or have the option to guard again. If Howard draws, then the play is into the middle with a centre guard and likely a good position for Koe to force a single. Continually attempting run backs is generally counter-intuitive to what a team one up without in the second last end wants to do: force the play to the centre and force the opponent to a single and have a 75% or better chance in the last end – with a risk of giving up a deuce and having a 40% chance coming home. The small chance to steal one, leaving Howard a 12% to win, also supports a draw strategy. In Koe’s defense, playing to avoid a three was perhaps his motive and they were comfortable with that style. It is a case where the risk of a three is minute compared to the great advantage of forcing one or stealing – but sometimes it’s difficult for a team to want to take additional risk if they feel it could take them out of the game. Let’s attempt to analyze the shot call. This involves VERY rough estimates of final outcomes, but allows us to examine how to reach a decision.

Draw:
Koe steals = .1
Howard scores one = .4
Howard scores two = .3
Howard scores three = .2

W (Koe) = 53%

Koe chose the hit, which ultimately resulted in two. Let’s estimate what outcomes may have been most likely:

Hit:
Blank = .1
Koe steals = 0
Howard scores one = .3
Howard scores two = .6
Howard scores three = 0

W (Koe) = 53%.

If Howard scores a deuce more than 60%, then Koe wins less than 53%. The decision appears close. Ultimately, it depends on Koe’s estimation of Howard’s chance at scoring 3 and ensuring that Howard never scores 3 when they attempt the run-backs. I would prefer the draw but it is closer than I had first thought.

Eighth End:
Blake’s first rock, they attempt to come around Howard’s stones staggered in front of the rings. An alternate play would be to double those top stones out and sit 2nd and 3rd shot. By playing to the middle it left a greater chance of only a single and increased chance of a steal. This is the style of play I suggested earlier Koe could have chosen in the 7th, but here the opposite is perhaps true and opening up the play may have increased his chance at a deuce and provided a greater chance at a single if he needed a draw on his last.

A good game and one where a few more made shots on the part of Koe’s rink could have changed the outcome. Whether the decisions we’ve examined here may have had any difference is up to the reader to determine.

Until next month, Happy Halloween!

Team Martin Can’t Hold Down the Haggis

What is it that makes sports entertaining? Is it watching the thrill in victory, or the agony of defeat? Do we admire and respect our sports figures for their immense talent and skill, something we do not possess, or for their ability to face the challenge and, sometimes, fail to over come it. Golf, baseball and, similarly curling, present a case for the latter. Do we remember Greg Norman for his heroic achievements at the British Open, or for his complete collapse at the 1996 Masters. The answer is pretty clear. By showing us the same frailty in their inability to overcome the tension of the moment, we see these stars are human. We share the same nervous anxiety when we stumble giving a presentation to a large audience, three-putt from ten feet for a $5 Nassau, or babble incoherently when asking the pretty girl to go on a date.

We still marvel at the feats of Tiger Woods or Michael Jordan, who may lose to an opponent who bests them on a certain day, but never seem to “choke” when the opportunity for greatness is at hand. Jack Nicklaus was the Greatest, but Arnold Palmer and his collapses in the US Open, Masters and PGA, along with his wins, make him “The King”. Something to me is very appealing in experiencing these moments of sport. Moments with a Greg Norman, Jean Van De Velde, Kenny Perry and, yes, a Kevin Martin.

Kevin Martin does not have the records in world competition that anyone would expect from (arguably) the greatest pure curler this country has produced. Kevin Martin beats EVERYONE. Regardless of his team, Kevin has been at the top of Men’s Curling for almost twenty years. He simply Wins. Against every team, at every event….except on the World stage. Is it something more than poor ice, off-days or random chance?

In watching Team Canada’s struggles against Scotland in each game they played, I was trying to determine if it was more Scotland playing great or Canada flat. It was clear Scotland took Canada off their game and disrupted their rhythm. Unlike other games the past two seasons, Kevin never appeared to have a clear sense of his strategy or an ability to dictate the flow of play in each game. In the finals, they looked to have this solved, but the final end proved otherwise.

Most of the discussion in future years, over a cold one at the local rink, will be the call to throw first skip stone away. This shot does appear bizarre and I prefer the option to drive the top yellow stone into the pile – but this is more an opinion versus a fact. Kevin made a very difficult choice, one he must have known would be scrutinized for the remainder of his life and beyond. However, on his last shot, he had two possible options, both likely better than 50%, to win the World Championship. I believe a different choice could have left him a better chance or possibly made Murdoch’s last more difficult, bringing the chance of a hand shake before the final rock. However, several options, such as a guard or a slightly missed hit, could also have left Kevin with less than 50% chance to win. It is my opinion Kevin could do better choosing an alternate shot call. It is a fact that with second’s first stone in this situation: peel the guards. Why does Kevin Martin call Marc Kennedy to play a soft hit and roll into the four foot, when two centre guards sit covering the four foot, in the final end, when tied with hammer? I suspect two things may have led to this critical mistake:

Martin “felt” a need to play a more aggressive end. This could be similar to the Brier final in 1997 against Vic Peters, played during the 3-rock free-guard zone era. I can’t recall the specifics, but the final score was 10-8 and Martin had an option to play a conservative final end, but instead chose to be aggressive.

Kevin strategically “choked”. After months of curling, against the best teams in the world, and the hours of practice and preparation, the culmination of a season comes down to the final end. Similar to Kenny Perry, seeing a two stroke lead with two holes the play, he begins to picture the win. The fatigue combined with the enormity of the moment, leads to a mental breakdown at a critical point. Instead of focusing energies on the job at hand: the shot, the putt or the pitch – just as they would normally - the curler, golfer or ballplayer starts to see themselves winning. In an interview with Scott Hoch during the recent CBS Masters telecast, referring to the missed 2 foot putt from 20 years previous, Scott stated he saw himself in the green jacket and could not focus on what he needed to do, get the ball into the hole. Kenny Perry said in his Saturday press conference, when asked what it would feel like to win, that he wasn’t going to answer the question – he needed to stay in the moment. He did for 70 holes, and then his crisp draws turned into evil hooks and his right hand got twitchy. These golfers have both won many tournaments, just as Kevin has, but when the title that they REALLY want to win, The Masters, was close at hand, they got out of their routine, out of tempo and performed well below their ability.

I obviously can’t say if the latter was the case. Kevin has been in similar pressure situations many times and shown the ability to overcome these nerves. From my vantage point, and my analysis of the three games played, something with team Martin just didn’t seem right when matched against Scotland. They did not look like the same team that plowed through Canada’s best all year. It seemed to be more than simply shot making. I expect Team Martin will prepare, focus and do all they can to ensure next time to execute to their peak ability and with clear thinking, when the “moment” happens again.

Some other notes from the recent Mens’ World Championships:

1. Thanks to TSN for the extreme close up of the antique measuring device (and the CCA logo) being used for a World Championship. At a critical point in the game, the Swiss were held to a single when their second rock was deemed “tied” with Norway’s. The gaps in the measuring device were similar to those dial kitchen timers from the 60s. Can’t these enormous prices for tickets go to support some digital devices? If not, at least get someone to “sharpie” some extra lines on the dial so this fiasco doesn’t happen again.
2. No thanks to TSN for constantly missing the leads rocks. Fine, if you need to come back late in the early ends, but in the final end of the final game we missed the first 3 rocks of the end. That’s 18.75% of the end. And the tick attempt in a tied game is perhaps the second most critical shot of the end (other than skips last). Makes it even harder for me to analyze calls if I don’t know what was played. Ray did fill us in on occasion, which is helpful. 
3. In the 3-4 Game, Norway chose not to play a corner guard when one down with hammer and Switzerland came into the rings in the 7th end. They played out for a blank. My February article examined the interesting position in the 8th end, where a blank or taking one is essentially the same, but what about the 7th end? In the 7th, Norway has a 40% chance to win when one down with hammer. After they blank, their chance in the 8th is 38%. If they play aggressive and are held to one, they are 35% playing 8th. If this happens in 8, they are 34% starting the 9th end. Doesn’t appear to be a poor decision. What does 3 do? If Norway takes 3 in the 7th, they are in Control with 79% chance. A three in the 8th moves them into Dominant Control and 85% chance to win. I like to stay aggressive, and might prefer to play a corner – but there appears to be some reasoning behind their decision.
4. Another example of strange events for Team Canada. In the 1-2 game, Martin is down one without playing the 8th end. John’s rock doesn’t quite move the Scotland stone far enough, and they lay second. On Kevin’s first shot, they elect to guard. I’d suggest this is a position where greater risk could be taken. Kevin may have thought he’d have something on his next shot – but let’s assume he knew he would not and he is playing out the end to force Scotland to one. Two down with and two ends remaining,. Martin will win 15% of the time. If you’re wondering if Kevin’s numbers are better than our average statistics, they’re not. The Martin team is statistically in line with these numbers. If you add in the small chance Scotland manages a deuce in the end, the 15% is actually high. I would have preferred Kevin to play aggressively for a steal, even at the risk of a big end. He needs to steal 44% of the time to make the risk statistically correct. Clearly he felt his chances weren’t that high – or possibly that he’d have a chance with his last shot. Strange that they were unable to see what Scotland’s shot would leave them – similar to the 10th end in the finals.
5. In the 10th end when tied – tick, tick, peel, peel and then, when in doubt, peel some more. Then draw for the win. Anything else, in my opinion, increases your risk of losing. Did you notice that Marc made both his shots called and his Scotland counterpart missed his – and they lost.
6. Thanks to Scotland for great play and great strategy (long guards, attempting to minimize run-back opportunities for Canada).
7. And thanks for the drama. In the words of Jim Nantz “ It was a World Finals unlike any other”. Amen.

Brier Notes: Martin’s Math Test

During his round robin game with Ontario, Kevin Martin says to TSN: “It’s a real Math Test out there!” Could he perhaps be a fan of this blog? Does he have his own computer programs to analyze data? What goes on in his mind during a game and will he share it with us some day?

Kevin in my opinion appears to make more correct decisions, and in a quicker and more decisive manner, than any other skip. It doesn’t hurt that he and his team have missed very few shots in the last two years either.

I had a great time at the Brier, if only for one afternoon and at the patch later that evening. I’ve finally reviewed all of the Tivo recordings I made from the event, and have started to gather some random thoughts and ideas. I may yet come back to a specific situation again, but for now, below are some non-sensible ramblings.

1. “It’s a Math Test out there”. Says Kevin Martin to Cathy Gautier of TSN at the 5th end break of his round robin game with Ontario. Simply one of the finest games I’ve seen in years, perhaps only rivaled by their rematch in the 1-2 game. Condolences to Steve Lobel. That makes it 9 years in a row in our “My Home Province vs Your Home Province Bet”. I’m looking foreword to eating some of those Toronto Pork Chops.

An interesting situation developed in the 9th end. Ontario leads 5-4 and Alberta has the hammer. Forgive me if I’ve stated this before, this is the best time in the game to be one up without. Howard will aggressively attempt to steal (90% chance to win) or force Martin to a single (74% chance to win), at the risk of giving up a deuce, where they still have a 38% chance to comeback and win in the 10th end. Martin is sitting one, with a Howard stone covering it in the rings. Howard begins placing centre guards and Martin is peeling these guards. For some observers, this could appear a strange situation. Why is Ontario guarding when their opponent is sitting one and they are up one? With 7 stones remaining, John Morris is about to throw a peel, when he heads down to the other end to discuss with Kevin and they instead decide to draw into the rings. Howard actually avoids giving up three, but surrenders a deuce. He is unable to score his deuce in the 10th end and Alberta wins.

I did not like Howard’s decision to play a guard on Richard’s first stone and, regardless of outcome, Martin’s decision to draw seemed correct. How might we analyze this situation mathematically?

Let’s assume a peel will result in either a blank or Martin being forced to one. I suspect if that Ontario would have tried a soft hit and roll to split the rings and lie two with Richard’s next shot. This would have forced Alberta to make a double in order to blank. We’ll estimate a blank 80% of the time – i.e. where the rocks were lined up, given three chances, Martin will clear the rings 4 in 5 tries.

W = (1-.74)(.2) + (.38)(.8) = 35.8%

With a come around, there are several rocks to come and difficult for us to determine outcome. Clearly, a blank will not occur, we need to estimate what the odds are Martin is able to score two (let’s assume no three is scored) versus a steal or held to one. We need to come up with Variables, which are estimates of an outcome.

X = Howard steals one
Y = Martin takes one
Z = Martin takes two

W = x(1-.9) + y(1-.74) + z(1-.38)

Initially, let’s assume Howard doesn’t steal. Set W to .358 and y=(1-z) and solve for Z

.358 = (1-z)(.26) + z(.62)

Z = .281

Assuming Howard does not steal, we need to expect a deuce 28% of the time, in order for the draw to be the correct call. Factoring for a possible steal, let’s suggest that at least 1/3rd of the time we need to score two. Is that the case given Martin’s team, a guard and shot stone? I suspect it is, but that is up to Martin to decide. Adding in even a slight chance for three, and 90% chance to win, it is very favorable to take the risk now. Thinking ahead, Martin would consider Howard’s likely call on Richard’s last stone and his chances of blanking when that occurs.

What should Howard do? Perhaps placing the guard off-centre on the other side of the four foot and giving themselves an open shot at their stone may have provided more options for them. Depending where John’s stone landed, Rich would have a potential double or at least a hit to lie 2nd and 3rd with rocks in good position above the four foot. I am more inclined to have Rich hit and roll to lie two and take the chance Martin is unable to double them out for a blank. Worst case is you are 1 up coming home and 62% likely to win. I expect Glenn, like many teams, expect Martin to score his deuce more often than 40% - and this could weigh in his decision to play the 9th more aggressively than he may have given another opponent. I will continue to argue the case that Martin has no more than a slight advantage over 38% against a team of Howard’s ability. Our study of Grand Slam events supports this argument – but it remains an argument where some will always side against the numbers. Good luck to those who choose luck as the basis for their strategy.

2. Further evidence that Kevin Martin either reads my articles, studies the math himself, or has the best instinct in the game. On not one but two occasions, Martin chose to bring his first rock into the rings when tied with hammer and without last rock in the 8th end. Martin did this against both Gushue and in the 1-2 game against Howard. Incidentally, in the 1-2 game he placed a centre just the end before in the 7th, when tied without hammer. This decision was discussed in my January article.

3. It is the 1-2 game, 7th end. Howard is tied with hammer. On Kennedy’s last rock, Howard has a single corner in play and Kevin yells down “play for a blank? I don’t know”. They decide to play a tight centre guard and Howard continues his conservative play in the end by peeling. Martin then has John draw around the corner on his first rock. In this situation, Howard can go from a 65% chance if he blanks to an 80% chance by scoring two. A steal puts him at 38%; take one they are 62%. If, however, he blanks, the outcome in 8 of two is 85% compared to 66%. I’m not certain I agree with Glenn’s approach in 7 at that stage. Coming around the centre would have forced the end, increasing a chance for multiple score. The added risk of a steal is not as bad in this end (7th) as it would be in the next. I’d like to examine this end further, but it’s late and I’m tired. Perhaps another day…

4. The 3-4 game with Manitoba versus Stoughton. Linda comments in the 8th end that Gushue wants to force Stoughton to 1, he doesn’t need a steal. Granted he does not HAVE to steal but to imply he is not playing for a steal is foolish. If Stoughton takes one, Gushue has a 15% statistical chance to win. If he can steal, his chance increases to 34%. In the 9th end, Stoughton chooses to play a run back from outside the rings on his first rock. Linda states he “has to”. I don’t agree has to. In fact, he could play a draw on his first stone. He could have put his rocks in a position where Brad would likely guard again and steal a single, putting Stoughton 1 down in 10 with last rock. The draw could protect Manitoba from what nearly occurred, a steal of two. In the 10th end, Stoughton made a fantastic shot. But with more time, Gushue may have examined the option of coming into the rings for second shot. An option which, though not eliminating the outcome, may have made Stoughton’s shot either more difficult or only to tie. They both came close to running out of time, something I can’t remember seeing at a game of that level in a very long time.

Scotties Decision by Team Canada and Middle Game Strategy

Jennifer Jones’ Team Canada rink made some interesting decisions in their round robin game against Ontario at the 2009 Scott Tournament of Hearts (Scotties). During the 6th end, Team Canada (TC), one down without hammer, could have chosen a more aggressive route during the latter part of the end. Instead of drawing around their opponent’s stones in front of the rings, they instead chose to hit the Ontario stone towards the back of the rings and play out the end as a blank. Was this the correct decision? Recall:

Notice that if the end is blanked, TC has a 24% chance. At the beginning of the 6th they had a 22%. In fact, their odds get slightly better if the end is blanked.

If they play aggressive and steal, they increase their chances to 40%. Holding Ontario to one is 22%. In fact, a blank appears to be 2% better than actually forcing Ontario to a single point! It appears the risk of attempting a steal at this stage is not necessary.

What about in the next end? If it had been the 7th instead of 6th end, the decision is very different. Now, entering the 8th end when 1 down without hammer, the odds are only 18%. Holding Ontario to a single gives a 21% chance. A steal in 7 instead of 6 still leaves them 40% - no change. It would be more tempting to play the final rocks aggressively if it were the 7th end. If the 7th were to be blanked and TC is one down without hammer playing 8, it is imperative to either score a steal or force opponent to a single. When entering the final two ends 1 down without hammer, a teams chance drops to 16% - but more importantly, a steal in 9 gains less. A steal in 8 would produce a tie and a 39% chance, but a steal in the 9th to tie the game is only 30%.

The 5th and 8th Ends
Recall my previous article on Early, Middle and End Game. The Early Game is the first 4 (or 2) ends. At this stage, most top teams will play aggressive attempting to take control or dominant control as soon as possible. In the End Game (final 3 ends), teams will play the scoreboard more closely, attempting to be tied with hammer or two up without hammer in the final end of a close game. So what is Middle Game Strategy?

Middle Game is the 5th through 7th ends in a ten end game (or 3-5th in an 8 end game). Recalling my previous description, statistical changes start to appear in the middle game. Trends appear for each situation (tied with hammer, 1 up without, etc). So what are some considerations when determining our Middle Game Strategy?

The first decision is whether to continue aggressive play. This is usually the case early in each end, but as the end develops a team will choose shot calls based more on scoreboard and ends remaining before the End game. So to start discussion on Middle Game strategy, let’s start by examining which scenarios are more favorable in the End Game.

I will use a 10 end game from now on, the reduce complication. To transfer this analysis to an 8 end game, just subtract 2.

In the 9th End, one down with hammer is a disadvantage greater than any other point in the game. In fact, only the scenarios starting the 9th and 6th ends have tied without hammer the same (less than 1%) as one down with hammer. In all other cases, one down with hammer is preferred position. If we have the hammer in a close game the ends previous (5th and 8th), it allows us to take some additional risk with less penalty for being forced to a single point. Recall a Close game is one in which a team is down one with hammer anytime or tied prior to final two ends.

One down with hammer:
In the 5th and 8th ends we can aggressively play for two or three and if we are forced to one, our chances are actually the same as if we had blanked the end. If we instead are one down with hammer in other ends, if our aggression results in being held to one, we are worse than if we blanked the end.

One up without hammer:
Conversely, forcing our opponent to one in this situation (5th or 8th end) gains no advantage over blanking the end. The risk of playing aggressive to force our opponent to one, which may result in a deuce, provides no advantage – a steal is required to gain any advantage. Stealing in the 5th puts us at a 76% winning probability (Control). Stealing in the 8th an 85% chance (Dominant Control). Blanking 5 and then stealing in the 6th in fact gives us now an 80% chance. I’d suggest a sensible play is to tempt our opponent into blanking the 5th end and force our position without hammer in the next end. Blanking the 8th was discussed in our last article and is more open to debate.

Tied without hammer:
If we force our opponent to a single, we again gain no advantage to blanking. However, a steal is a significant advantage over our current position. For the 5th end, in our previous example (one up without) a steal takes us from a 61% chance to 76%. If we are tied and steal, we move from 39% to 61%. Using our analysis from the last article, switching from 39 to 61 is 50% better, whereas 61 to 76 is only 25% better. For the 8th end we go from 34 to 65 (91% better). It would appear we are more inclined to attempt to steal in this scenario. However, stealing is always difficult and we risk our opponent making a multiple score. We are forced to be more aggressive because of our position but being one down with hammer gives us an ability to be aggressive without the same risk.

Tied with hammer:
Being forced to one in the 5th or 8th end is no mathematically disadvantage. In all other ends, being held to one is a disadvantage over a blank. Again, per situation one down, we can be very aggressive at the risk of being held to one. However, as pointed out above, a steal is very bad for us in this position. In fact, a steal is very bad for us every time in this position. It is most critical in the 9th where we drop from 74% to 38%.

In every case, having hammer appears to be a greater advantage in this position. We can be aggressive without any risk of being “held to a single” as it is virtually no different mathematically from a blank.

So…what is our finding? In a close game, we’d prefer to have hammer in the 5th and 8th ends. We may in fact make decisions in the ends previous which will force this situation. For example, if we are tied playing the 4th with hammer and have an opportunity to blank, we are more inclined to take this route. If we are one up in the 4th or 7th, we should force our opponent into scoring, even at the risk of a deuce, in order to have hammer in following end. Eight end games become interesting because the advantage exists in the 3rd end. A team may even choose to tempt a blank if they are without hammer in the first end, to force their opponent to score in the second end, in order to have hammer in the third. This seems drastic and I’d suggest the advantage is not significant enough to “drop an end”. But further analysis might disprove my initial thinking.

Some readers may have noticed that there are two ends between the 5th and 8th. This means, without a blank or a steal, if we have hammer in one of these ends, our opponent has hammer in the other end. For example, say having hammer in the 5th when one down results in a deuce. We are now one up. If our opponent is held to one and then we are held to one, we are now one up without in the 8th end. However, if our opponent ties us in the 6th and we instead manage a blank in the 7th, we are now tied in the 8th with hammer.

I would not suggest this analysis should be a factor in how a team begins play in and end. The modern game does not allow a team to force a blank end at will. However, as an end develops we may be more inclined to “bail out” of certain ends in order to better position us in ends where we have greater advantage with hammer in a close game.

End Game Strategy: BDO Quarterfinal – Howard versus Burtnyk

There were several decisions made during the 6th and 7th ends of the 2009 BDO Quarterfinal between Glenn Howard and local favorite Kerry Burtnyk. This month I will attempt to breakdown some of the decisions and determine how math could be applied to each scenario or shot call to support or contradict the final decision.

The 6th End: Centre Guard
At this stage, the game is tied 4 -4 and Howard has the hammer. The 6th end is, per my definition, the beginning of the “End Game” (see November 2008 article). Statistics indicate that Burtnyk at the beginning of the 6th end (in an 8 end game) has a 35% chance to win. (Math whizzes may have already guessed Howard has a 65% chance).

Let’s begin by reviewing the probabilities that Burtnyk will win, based on various outcomes of the 6th end (percentage chance to win with two ends remaining):

With two ends remaining:
Tied without hammer (Howard blanks 6th) = 34%
Down one with hammer (Howard takes 1 in 6th) = 35%
Down two with hammer (Howard takes two in 6th) = 15%
Up one without hammer (Burtnyk steals in 6th) = 65%

The numbers indicate that holding Howard to a single, in the 6th end, is in fact not much different than a blank. This is NOT the case if Howard is forced to one in the 7th, the difference is 25% (if Howard maintains hammer) to 38% (if he is forced to one).

A steal, however, is a great advantage in the 6th (65%). In fact, it is the most mathematically advantageous point in the game in which to be up one without. At all other times, chances are 61% or less.

Let’s ask a few questions:
Should Burtnyk play a centre guard or place the first stone in the four-foot?

In the game, Garth Smith placed the first stone in front of the rings. I would suggest this is the incorrect call…and here is why…

If Burtnyk places the first rock in the rings, should Howard play for a blank or attempt to score a deuce?

Howard now has to determine if he will play a corner guard, using hammer aggressively in an attempt to score two (or more) or instead play out a blank. We’ve seen above a blank is identical to a single point. In fact, if Howard plays out for a blank and noses his final stone, there is statistically no difference!

There are few skips at this level that would not prefer to force the issue while they have hammer with 3 ends remaining. The key reason: a deuce results in a high probability of winning. Two up without hammer during the End Game is as follows:

Two Up without hammer wins:
1 End remaining = 90%
2 Ends remaining = 85%
3 Ends remaining = 80%
4 Ends = 80%
All earlier ends = 74-75%

Howard’s only reason to wait to the next end is for a 5% advantage – IF he is able to score a deuce. Is the difference of 85 to 90% enough to make up for the risk of sacrificing an end with hammer? I don’t believe it is, and here is why. Recall my article from Dec 2008 describing a game as Close or one team being in Control or Dominant. A deuce in the 6th or 7th end results in a Dominant position for Howard.

For those who understand how chip values change in a Poker tournament, a similar analysis can be used here. In a poker tournament, as you collect chips, each additional chip’s “value” is less than those previously acquired. For those interested in understanding this better, read David Sklansky’s “Tournament Poker for Advanced Players”.

Each percentage point in probability of winning becomes less important, the higher your chances are. The difference between having a 50% chance versus 55% is more important that 85% to 90%. Another way to examine this is the advantage in the first scenario is 10% better, but in the latter it is only 5.8%. Some readers may also note the contrary is true. A team that is behind sees a greater benefit from small percentage changes. The advantage of a 15% chance over a 10% probability is 50% better!

If Howard blanks the 6th and either team scores one in the 7th, the game remains “Close”. He has essentially given up an opportunity to take a Dominant position; with very little risk of Burtnyk taking it at this stage (unlikely Kerry will steal two).

Also, recall that being forced to 1 is fine in the 6th but not the desired outcome in the 7th. Howard should be more inclined to be aggressive in 6 where a single is more advantageous, whereas in the 7th he would then much prefer a blank to being forced to a single point.

So….
Given that Howard would statistically prefer not to blank and Burtnyk is statistically indifferent, Kerry should place the rock in the four-foot. If Howard chooses not to play a corner guard, by not making the correct play he is giving some (however slight) advantage to Kerry. The outcome for Burtnyk is good positioning for a possible steal and reduced chance for a deuce or worse.

However…
All of this analysis does imply that a team prefers to place a stone and then place a guard (after the corner) – rather than having your opponent draw to the four-foot and then corner freezing to their stone (eliminating the placement of a corner guard). Burtnyk may prefer not to have a corner in play and prefers positioning stones to the middle of the rings, even if Howard initially has shot rock. I’d be very interested in the perspective of that discussion.

The 6th End: Walchuk’s last shot
Burtnyk sits top eight (biting four-foot) and Howard sits to the side, biting the four, guarded by two of Kerry’s stones. Despite repeated rewinding on my Tivo, I could not determine who was shot. Howard also sits third and fourth.

Kerry called for a double run-back by Walchuk. He suggested it was either that or play the guard. The result was removal of the Howard stone and sitting two, but both guards were removed and Howard remained with 3rd and 4th shot. This call appeared to be conservative, attempting to lower the chance at 2 or 3 and increase the chances to force Howard to 1. A steal seemed very unlikely at that stage. It appeared a deuce was probable, but Richard missed his next shot. It is my opinion that, given the difficult position if Burtnyk gives up a deuce (15%), keeping the guards and pursuing a more aggressive strategy, with a higher chance at a steal would increase their chances to win. In either case, they were in a difficult spot. Making some very rough estimates of probable outcomes for both calls:

Double Run-back:
Howard take 1 = 60%
Howard take 2 = 30%
Blank = 10%

W = 28.6%

Guard
Howard take 1 = 50%
Howard take 2 = 40%
Burtnyk steal 1 = 10%

W = 30%

These estimates are highly debatable, given the number of rocks remaining. However, on the basis that a three or two has little difference at this stage (see my comments above regarding Dominant position). Kerry should be trying to avoid a deuce at all costs while also trying to steal (not an easy task). It is my opinion (perhaps not his or others) that removing the two guards greatly reduces a chance to steal and may in fact increase the chance for an easy deuce.

6th End, Burtnyk’s last rock
Kerry had an option to either draw around the centre guard and attempt a steal or remove the Howard stone and possibly roll behind cover and force Howard to a single. This is an interesting scenario. Per above, a steal is a significant advantage, but a deuce is also a huge risk at this stage of the game. A single by Howard or blank has virtually no difference mathematically. In fact, it was statistically irrelevant for Burtnyk to spend extra effort in attempting to roll their rock behind cover – either outcome produces the same mathematic result. Kerry might, however, determine an advantage to be either one down or tied. Also the added chance Glenn might miss his draw for one (however remote) could be considered a slight advantage in this situation. I want to stress that the mathematic analysis does not take into account other factors, ice conditions, opponent, etc, which Kerry may have considered.

Mathematically, how often would Kerry have to make a perfect draw for the steal attempt to be the correct call?

W = x(.65) + y(.35) + z(.15)

Where
x = chance of a steal
y = chance Howard takes one
z = chance Howard scores two

We know Burtnyk’s hit results in a likelihood of 35%, set W = .35

.35 = x(.65) + y(.35) + z(.15)

Let’s choose a value for y and solve for x.

We estimate y = .3. That is, Howard will score one 30% of the time

Z = 1 – (x + y) = .7 – x

.35 = x(.65) + .3(.35) + (.7-x)(.15)

X = 28%

Conclusion, if Burtnyk believes Howard will likely take one 30% of the time, he needs to be successful with a steal > 28% in order to attempt the draw. If he actually believes Howard may only score a single half the time, it drops to 20%. If instead you assume no single and either a steal or a deuce, he must be successful stealing > 40%. Ultimately there are many factors, amount of curl and length of guard being most critical.

I found it interesting that, debating whether or not to attempt a steal is an unclear decision. Meanwhile, the very capable commentating team of Mike and Joan (ranking above their TSN counterparts, in my humble opinion) were instead focused on Burtnyk possibly drawing to the back or playing a roll in order to force Howard to one. As we’ve pointed out above, this decision has no statistical impact!

6th End – Howard’s Last Rock
On Howard’s final stone, assuming Burtnyk’s rock was easily accessibly, should he draw for one or blank the end? As we’ve stated above, mathematically there is no difference. Ice conditions, your opponent and other factors would likely come into play.

I would be tempted to blank, but the decision is not as clear as some might suspect. Many teams could choose to draw for one and they may very well be correct. If your team can hit well and possibly clear the mess your opponent is likely to create in the 7th end, increasing potential for a blank in the 7th, blanking the 6th end might be your preference. If your team prefers aggression and is more comfortable forcing the issue without hammer, by all means take 1 in the 6th and attack in 7. Also, you may asses your opponent is stronger with hammer and would prefer to keep it. Or the opposite may be true, and their ability to set-up an end without hammer may be something you wish to avoid.

7th End – Playing the Blank with 7 rocks to go
In the 7th end, Burtnyk was faced with another interesting decision. One down with hammer and a corner guard. No other rocks in play. Third’s first stone. Rather than attempt a deuce (and risk being held to one or surrender a steal) they chose to peel and play for a blank.

Blank results in Burtnyk being one down with hammer and one end remaining.

W = 38%

How often would Burtnyk need to score a deuce in order to attempt a draw, rather than blank?

Let’s assume that if they attempt a draw around the corner, a steal or blank will not occur. Either Burtnyk is forced to a single or he scored a deuce.

x = Burtnyk takes 1
y = Burtnyk takes 2

.38 = x(.26) + y(.62)

x = 1 – y

.38 = (1-y)(.26) + (y)(.62)

y = 35%

Burtnyk will have to score a deuce greater than 35% of the time for the draw (rather than peel) to be correct. Some of our recent analysis indicates that top teams in fact win slightly more than 74% when tied in the final end. Combine this with some small chance of a steal, Burtnyk would need even greater confidence in his chances to score two.

Whew! That’s it for this month. Congrats and good wishes to Team Pahl (Alberta) and Team Lobel (Ontario) in qualifying for their respective provincials. And good luck to all readers of Curl with Math, whether you are chasing your first or fourteenth Purple Heart.